Nearly antipodal points or antipodes refer to the most geographically distant points on a sphere, that is, the points are diametrically opposite to each other. If a line is drawn between these two points, it passes through the center of the sphere and forms its diameter.

Computing the great circle distance between these two points is often a corner case for most geodesic computations, and the distance is either overestimated or underestimated. In case of Vincenty’s formulae, the solution fails to converge, or provides inaccurate results. This can have major implications in applications which rely on accurate results, such as flight navigation systems. The software can handle this either by doing an error analysis check and providing specific values through which the inaccuracy can be identified, or by choosing a different method altogether.

This post provides a general description of geodesic algorithms and shows their inaccuracy for nearly antipodal points in the Boost Geometry library. A solution is then proposed following the paper Algorithm for geodesics, by Charles Karney, the implementation for which is provided in the GeographicLib library.

Problem description

The algorithms described below model the Earth as an ellipsoid, which is obtained by deforming a sphere by means of directional scalings, or more generally, of an affine transformation.

Geodesics algorithms are employed for solving the direct and inverse geodetic problems.

Direct and inverse geodesic problems

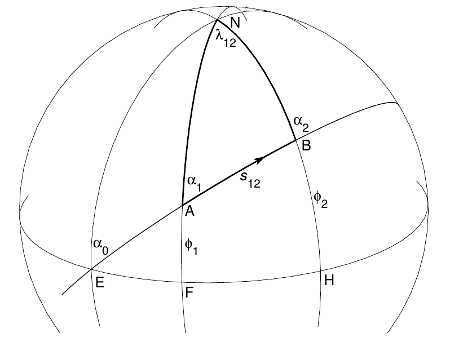
Our goal in the direct geodesic problem is to find the longitudinal difference $\lambda12$, the latitude $\phi2$, and the azimuth $\alpha2$ for the second point. The information we are provided for solving this is the latitude $\phi1$ and azimuth $\alpha1$ at the first point, and the distance between the two points $s12$.

On the contrary, the inverse geodesic problem deals with finding the azimuths for the two points $\alpha1$ and $\alpha2$, and the distance between them $s12$. The input data includes the latitudes for the two points $\phi1$ and $\phi2$, and their longitudinal difference $\lambda12$.

The direct or forward geodesic problem is much simpler than the inverse or backward problem because the equatorial azimuth $\alpha0$ can be determined directly from the given quantities $\phi1$ and $\alpha1$. However, the inverse problem is intrinsically more complex. In this case, the angle given by the longitude of $B$ relative to $A$ ($\lambda12$) is related to the corresponding angle on the auxiliary sphere $\omega12$ via an unknown equatorial azimuth $\alpha0$. This is shown in the figure below.

Over the years, numerous algorithms have been proposed for solving the above problems. The solution proposed by Vincenty (1975) is based on the series expansion carried out to third order in the flattening and provides an accuracy up to 0.1 millimeters for the WGS84 ellipsoid, however, as noted above, the inverse method fails to converge for nearly antipodal points.

In the paper Algorithm for geodesics, authored by Charles Karney, a solution is provided for direct and inverse methods that is accurate up to 15 nanometers. It continues the series expansions to sixth order $O(f^6)$ which suffices to provide full double precision accuracy for $|f| \leq \frac{1}{50}$, where $f$ is the flattening of the ellipsoid and is given by:

$$f = (a - b) / a.$$

Where $a$ defines the equatorial radius, and $b$ refers to the polar radius.

For solving the inverse problem, it employs the Newton’s method for adjusting $\alpha1$ until the correct $\lambda12$ is obtained. This typically requires two to four iterations and works for all types of input. Whereas, Vincenty’s solution can require thousands of iterations before it converges.

Problem demonstration

The strategies currently offered by Boost Geometry, also known as Generic Geometry Library (GGL) do not correctly handle corner cases for nearly antipodal points. To illustrate this, we select two points and compare their result with the GeographicLib library.

Inaccuracy in inverse problem

For comparing the results, we select two geographically distant points on the Earth’s surface which are almost diametrically opposite to each other i.e. they are nearly antipodal. The values below are represented in latitude / longitude pairs (degrees).

2.179167    -73.787500
-2.162200    106.139064

Using Vincenty’s strategy to compute the distance:

#include <boost/geometry.hpp>

using namespace boost::geometry;

typedef model::point
    <double, 2, cs::spherical_equatorial
    <degree>> spherical_point;
typedef srs::spheroid<double> stype;

// Define the strategy.
typedef strategy::distance::vincenty<stype> vincenty_type;

spherical_point point1(-73.787500, 2.179167),
                point2(106.139064, -2.162200);

// The distance is returned in meters.
double d = distance(point1, point2, vincenty_type());

Note: Boost Geometry’s convention is that coordinate values of 2D tuple are given according to mathematical axis order: X, Y. In terms of geographic coordinate system: longitude, latitude. For a detailed explanation, refer to the Design Rationale.

The distance returned is 19963713.360 meters.

Note: The reason we get a result in Boost Geometry is due to the BOOST_GEOMETRY_DETAIL_VINCENTY_MAX_STEPS macro which terminates the loop after a certain number of iterations. Otherwise, the solution may never converge.

We compare the previous result with GeographicLib which correctly handles the case for nearly antipodal points.

#include <GeographicLib/Geodesic.hpp>

using namespace GeographicLib;

const Geodesic& geod = Geodesic::WGS84();
double distance;

geod.Inverse(2.179167, -73.787500, -2.162200, 106.13906, distance);

Alternatively, the CLI tool GeodSolve can be passed the latitude and longitude positions of the two points. The -i flag refers to the inverse problem.

GeodSolve -i <<< "2.179167 -73.787500 -2.162200 106.13906"

This returns the distance as 20001571.083 meters. Thus, the distance computed using Boost Geometry was off my 37857.723 meters.

Inaccuracy in direct problem

To illustrate the problem with the current implementation of direct Vincenty strategy, we use the latitude and longitude positions of our first pair of points we used earlier, and try to recover the latitude and longitude positions for the second pair or destination.

In Boost Geometry, the direct strategy can be specified as follows.

#include <boost/geometry.hpp>

using namespace boost::geometry;

// For storing the resulting values.
formula::result_direct<double> result;

// WGS-84 spheroid.
srs::spheroid<double> spheroid(6378137.0, 6356752.3142451793);

// Define the strategy.
typedef formula::vincenty_direct<double, true, true, true, true> vincenty_direct_type;

result = vincenty_direct_type::apply(-73.787500, 2.179167, 20001571.135, 6.80724316, spheroid);

This gives us the latitude and longitude positions as 0.962372 and -76.9321, respectively. We again compare this with GeographicLib.

#include <GeographicLib/Geodesic.hpp>

using namespace GeographicLib;

const Geodesic& geod = Geodesic::WGS84();
double lat2, lon2;

geod.Direct(2.179167, -73.787500, 6.80724316, 20001571.135, lat2, lon2);

To use the GeodSolve CLI tool, drop the -i flag, which then defaults to the direct geodesic problem.

GeodSolve <<< "2.179167 -73.787500 6.80724316 20001571.135"

The resulting values for latitude and longitude positions are -2.16220000 and 106.13906400, respectively. Thus, we can see that the result provided by GeographicLib is almost identical to our input points (second pair), whereas, the result provided by Boost Geometry provides incorrect values.

Google Summer of Code 2018 project

Several issues have been raised over the past few years relating with the inaccuracy of geodesic algorithms in Boost Geometry for nearly antipodal points. The relevant tickets can be found at Boost SVN (#11917, #11929) and GitHub (#426, #449).

This project has been selected as part of the Google Summer of Code program under the Boost C++ organization. I will work under the supervision of my mentor Vissarion Fisikopoulos and co-mentor Adam Wulkiewicz, and implement the method proposed by Charles Karney in his paper Algorithm for geodesics.

The project proposal goes into the mathematical details of the algorithm along with the proposed timeline. During this period, I will provide my code in the BoostGSoC18/geometry GitHub repository which will be later on merged with boostorg/geometry repository.