As documented in the tile distortion issue section, the previous technique for drawing HiPS tiles brings some astrometry offsets for distorted tiles.

An example of such distortions can be viewed at this link (uncheck “Activate deformations reduction algorithm” to view the astrometry offsets): http://cds.unistra.fr/~boch/AL/test-reduce-deformations2.html

To overcome this issue, the parent tile is divided into four children tiles if it meets the following two criteria:

• One edge is greater than 300 pixels when projected
• Or, the ratio of smaller diagonal on larger diagonal is smaller than 0.7 and one of the diagonal is greater than 150 pixels when projected

For handling these checks, a function is_tile_distorted is introduced:

def is_tile_distorted(corners: tuple) -> bool:
    """Is the tile with the given corners distorted?"""
    edges, diagonals = measure_tile_lengths(corners)
    diagonal_ratio = min(diagonals) / max(diagonals)

    return bool(
        max(edges) > 300 or
        max(diagonals) > 150 or
        diagonal_ratio < 0.7
    )

The measure_tile_lengths function computes the length of tile edges and diagonals by computing the euclidean distance between two points, its source code can be found here.

If a tile passes the conditions specified above, it is then split into four children tiles, which is achieved by the following Python property:

@property
def children(self) -> List['HipsTile']:
"""Create four children tiles from parent tile."""
w = self.data.shape[0] // 2
data = [
   self.data[w: w * 2, 0: w],
   self.data[0: w, 0: w],
   self.data[w: w * 2, w: w * 2],
   self.data[0: w, w: w * 2]
]

tiles = []
for idx in range(4):
meta = HipsTileMeta(
   self.meta.order + 1,
   self.meta.ipix * 4 + idx,
   self.meta.file_format,
   self.meta.frame,
   len(data[0])
)
tile = self.from_numpy(meta, data[idx])
tiles.append(tile)

return tiles

The criteria for choosing the HiPS order and ipix for children tiles is mentioned in the HiPS IVOA paper, Appendix, page 31.

A Jupyter notebook illustrating this functionality can be found here. Currently, there is no recursion involved in tile splitting, so the parent tile is split only once. Therefore, the results can be further improved, a side-by-side comparison is shown in this GIF image:

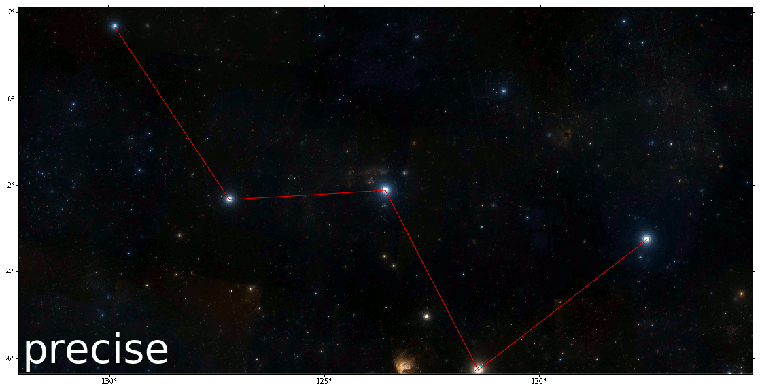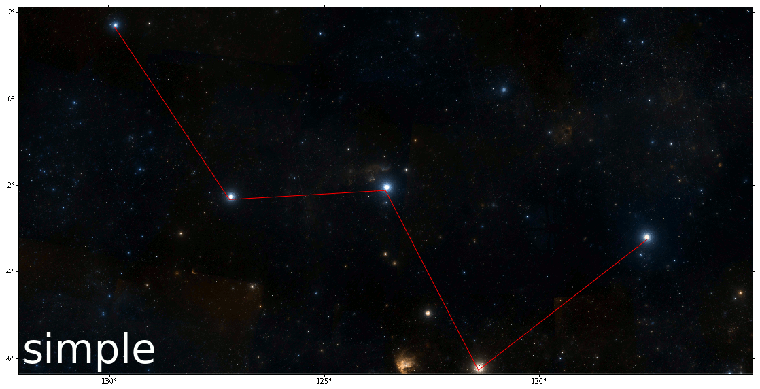
The red line connects five stars, of which the middle one is the Gamma Cassiopeiae. This can be used to verfiy if the image is drawn correctly, by looking at the corner positions and confirming if they align correctly with the stars.